深入理解计算机系统 | 学习笔记（五）

一、布尔代数

二进制值是计算机编码、存储和操作信息的核心，所以围绕数值 0 和 1 的研究已经演化出了丰富的数学知识体系。其中影响最深的代数体系是布尔代数，数学家布尔注意到通过将逻辑值 TRUE（真）和 FALSE（假）编码为二进制值 1 和 0，能够设计出一种代数，以研究逻辑推理的基本原则。

布尔运算

最简单的布尔代数是在二元集合 {0，1} 基础上的定义，它定义了四种布尔运算法则：

布尔代数的运算

上图中：

~运算符表示非操作，非真就是假，非假就是真。

&运算符表示且操作，只有两者同时为真的时候，运算结果才为真。

|运算符表示或操作，只要两者之中有一个为真，运算结果则为真。

^运算符表示异或操作，只有两者不相同时，运算结果为真（两者相同，运算结果则为假）。

位向量运算

布尔运算规定了两个命题之间的逻辑运算，因此我们可以 4 个布尔运算扩展到位向量的运算，位向量就是有固定长度为 w、由 0 和 1 组成的串。也就是有两个长度为 w 的位向量，分别命名为 a 和 b，那么两者的布尔四则运算表示的是向量位中每一个位对应的相应原算。

假设 w = 4，参数 a =[0110]，b =[1100]。那么 4 种运算 a & b、a | b、a ^ b 和 ~b 分别得到以下结果：

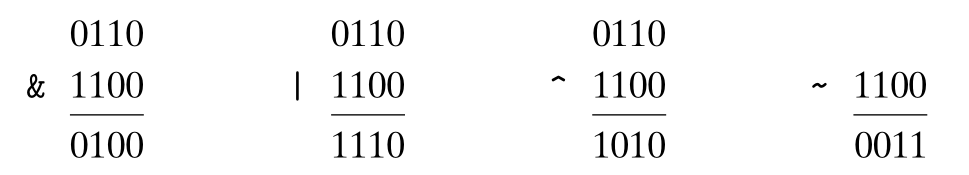
位向量运算

在大量实际应用中，我们都能看到用位向量来对集合编码。例如，在第 8 章，我们会看到有很多不同的信号会中断程序执行。我们能够通过指定一个位向量掩码，有选择地使能或是不能屏蔽一些信号，其中某一位位置上为 1 时，表明信号 i 是有效的，而 0 表明该信号是被屏蔽的。因而，这个掩码表示的就是设置为有效信号的集合。

二、C 语言中的位级运算

C 语言中有个很有用的特性就是支持按位布尔运算：

|就是 OR（或），

&就是 AND（与），

~就是 NOT（取反），

^就是 EXCLUSIVE-OR（异或）

C 语言中的位级运算可以运用到任何“整型”的数据类型上，下图是 C 语言中的位级运算实例：

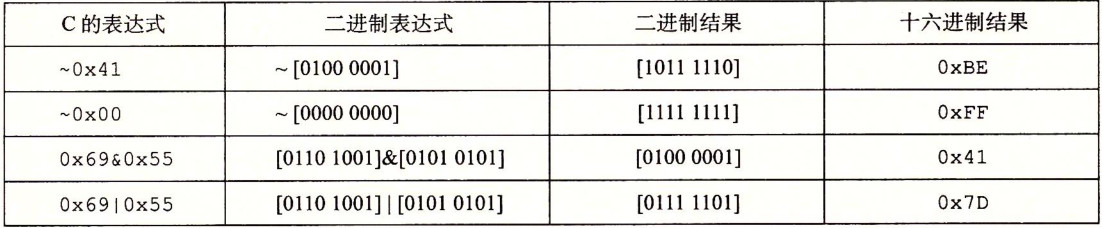
C语言中的位级运算

从上图可以看出，如果想要对数字进行位级运算，就需要将运算的数转换成二进制进行计算，计算出二进制结果再转成原来的进制数即可。

位级运算的一个常见用法就是实现掩码运算，这里掩码是一个位模式，表示从一个字中选出的位的集合。比如我们知道一个整数 x，如果我们想取得这个整数的最后一个字节的整数值的话，就可以采用位运算。

#include <stdio.h>

int main(){
     unsigned int i = 0x1234;
     unsigned int j = 0xFF;
     unsigned int k = i & j;
     printf("%X",k);
}

输出打印结果为：34，用图来理解掩码0xFF在运算过程中发挥的作用：

掩码运算

三、C 语言中的逻辑运算

除了位级运算，C 语言还提供了一组逻辑运算法则，分别对应数学上的命题逻辑中的 OR、AND、NOT。逻辑运算和位级运算容易概念混淆，在逻辑运算中只要是非零的参数，都表示位 TRUE。

||运算符表示逻辑与（OR）

&&运算符表示逻辑且（AND）

！运算符表示逻辑非（NOT）

注意：&&表示的是逻辑与的关系，如果第一个参数的结果为 FALSE，则运算符后面的表达式就不会再计算了，这一点和位级的与（&）不一样，位级的与操作是在位级别的与操作。！表示的是逻辑上的非关系，如果一个参数是非零，进行非操作之后得到的结果只是 1（因为 1 表示逻辑上的真）。

四、C 语言中的位移运算

C 语言中还提供了一组位移运算，向左或向右移动位模式。

左移：

C 表达式 x << k 会生成一个值。x 向左移动 k 位，丢弃最高的 k 位，并在右端补 k 个 0 。

右移：右移分为算术右移和逻辑右移。逻辑右移：x 向右移动 k 位，丢弃最低的 k 位，并在左端补 k 个 0 。算术右移是因为考虑到带符号的整数的运算：x 向右移动 k 位，丢弃最低的 k 位，并在左端补 k 个最高位的操作数（最高位是 1 就填充 1，最高位是 0 就填充 0，因为在有符号整数中最高位是符号的标识位）。

移位运算

几乎所有的编译器/机器组合都对有符号数使用算术右移，对于无符号数，右移必须是逻辑右移。

与 C 相比，Java 表达式有明确定义，表达式x>>k会将 x 算术右移 k 个位置，而x>>>k会对 x 做逻辑运算。

五、小结

计算机系统中出于高效率运行的考虑，信息的存储采用位的形式，并且使用简单的二进制组合形成不同的映射信息，光能存储还不能体现计算机的优势，它必须会计算数值，这也得益于数学概念的发展，计算机实现并拓展了布尔运算，使得计算机能够快递高效的计算数值运算。在布尔运算的完美实现基础之上，拓展到位级运算，再拓展到现实世界的逻辑运算和位移运算。

布尔运算提出了两位命题之间的四则运算：与（&）、或（|）、非（~）、异或（^），计算机中实现并拓展了布尔运算设计出位向量运算，使得 C 语言在设计之初就支持位级运算、逻辑运算和位移运算。